공부/통계학
[기초 통계학] 이산 확률 분포에서의 기댓값
728x90
반응형
개요
일반 데이터에서 평균을 구할 수 있듯이, 이산확률분포에서도 기댓값으로 중심 지표를 얻을 수 있고, 분산 등을 구할 수 있습니다.
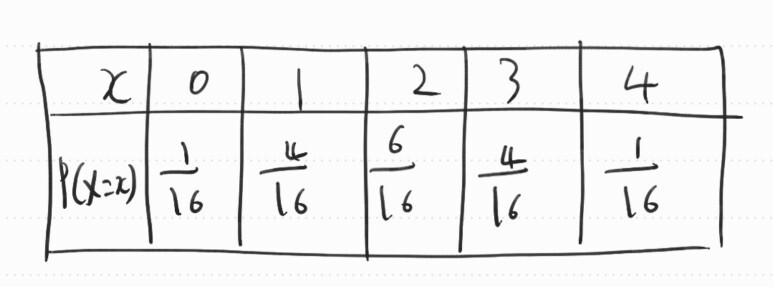
위와 같은 분포를 가지는 확률 분포 표를 해석해보면
2가 나올 확률이 가장 높고, 2를 중심으로 대칭을 이루는 그래프를 그려볼 수 있습니다.
위와 같은 분포에서도 기댓값과 분산 등을 구할 수 있는데, 기댓값에 대해서 알아보도록 하겠습니다.
확률분포에서의 기댓값
확률분포에서의 기댓값은 확률분포의 중심 지표라고 생각할 수 있습니다.
확률분포에서의 기댓값 구하는 방법
확률변수 x 값과 x가 나오는 확률의 값을 곱하는 것의 총합으로 구할 수 있습니다.
확률분포에서의 기댓값은 E(X)라고 나타냅니다.
기댓값은 아래와 같은 식을 통해서 구할 수 있습니다.

위 식을 해석하자면 확률변수 X와 X가 나올 확률을 1부터 N까지 곱한 값을 더한게 기댓값이라고 말할 수 있습니다.
즉 위쪽에 나와있는 표를 이용하여 평균을 구하자면,

평균은 위와 같이 구할 수 있습니다.
또 다른 예를 보자면, 아래 그림과 같습니다.

반응형
'공부 > 통계학' 카테고리의 다른 글
| [기초통계학] 기댓값(Expected value) (0) | 2021.10.28 |
|---|---|
| [기초 통계학] 확률변수에서의 분산 (0) | 2021.10.27 |
| [기초 통계학] 확률 변수(Random variable) (0) | 2021.10.25 |
| [기초 통계학] 사건의 독립성 (0) | 2021.10.24 |
| [기초 통계학] 조건부 확률(Conditional Probability) (0) | 2021.10.23 |

댓글