푸아송 분포 (Poisson distribution)
푸아송
푸아송 분포를 알기전에 우선 푸아송이 누구인지부터 알아봅시다.

위키백과를 찾아보니 프랑스의 수학자이자 물리학자네요!
이제, 푸아송이 만들어낸 푸아송분포에 대해서 알아봅시다.
푸아송 분포
푸아송 분포의 기본적인 의미는 특정 기간동안에 발생하는 사건 X에 관심이 있다는 것입니다.
예를 들면,
오전 9시에서 12시 사이에 발생한 휴대전화 통화의 갯수
오전 9시에서 10시 사이에서 매표소에 도착한 손님의 수
24시간동안에 본 강아지의 수
등이 있습니다.
여기서 확률변수 X는 특정 이벤트가 발생하는 것을 의미하겠죠.
자, 그러면 푸아송 분포의 확률 질량 함수를 한번 구해보죠.

위와 같은 그림이 있으면, 이 직사각형의 길이는 1입니다. 즉 푸아송 분포에서 특정 기간이라고 생각해봅시다.
그럼 이 특정 기간은 1의 길이를 가지겠죠?
우리가 관심이 있는건 이 특정한 1인 구간 동안에 발생하는 사건 X에 대해 관심이 있는 겁니다. X는 언제 발생할지 모르겠죠?
여기서 사건의 발생은 평균적으로 λ (람다)를 따른다고 가정해보죠. 람다는 0보다 커야합니다. 사건의 발생이기 때문에 음수가 나올 수는 없겠죠?
여기서 이 직사각형을 N개의 짧은 부구간으로 나눕시다. 이 부구간은 충분히 짧은 구간이라고 생각해봅시다.
여기에서 N이 충분히 많고 짧은 구간이라면 우리는 각 부구간에서 사건이 발생할 수 있다고 근사하여 생각할 수 있습니다.

각 부 구간에서 사건 X가 발생할 확률은 λ/N 라고 할 수 있습니다. 이유는 1인 구간을 N으로 나누었기 때문에, 각 구간에서의 평균적으로 사건의 발생 횟수는 λ/N 을 따른다고 할 수 있죠.
그리고 각 엄청 짧은 부구간에서 사건이 두번 이상 발생할 확률은 0이라고 생각할 수 있겠죠.
따라서, 각 부구간에서는 사건이 발생할수도 있고 안할수도 있게 되는거죠. 짧은 부구간에서 사건이 두 번이상 발생할 확률은 없으니까?
그럼 이제 어느정도 눈치를 채셨을거라고 생각합니다.
사건이 발생할수도 있고 안할수도 있다? ==> 이 말은 베르누이 시행을 의미합니다. 즉 성공과 실패 둘 중 하나인 실험이 발생하는거죠.
그런데, 이러한 베르누이 시행이 엄청 많은 짧은 부구간에서 발생하게 됩니다. 이는 분명 우리가 봤던 이항분포와 똑같은 의미를 가지게 됩니다. 베르누이 시행이 여러번 수행되면 그 분포는 이항분포를 따르니까요!
그러면, 우리는 여기서 이항분포에서 실험의 횟수인 N을 엄청 많이 하게 되는거겠죠? 그러만 수식은 아래와 같게 됩니다.
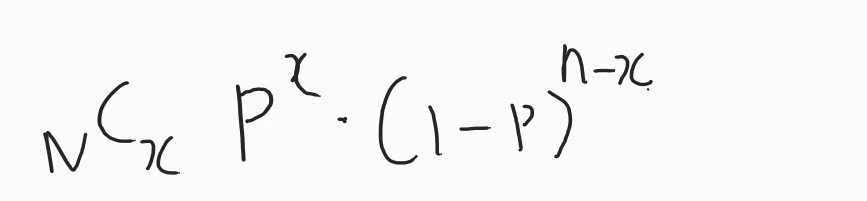
N은 실험의 횟수
X는 사건 발생의 횟수
P는 사건 발생 확률
1-P는 사건이 발생하지 않을 확률을 의미하겠죠.
여기서 N을 무한대로 보내게 된다면, 푸아송 분포를 따르게 되는겁니다. 특정 구간에서의 사건 발생횟수를 의미하게 되는거니까요!
여기서 N을 무한대로 보내보죠.
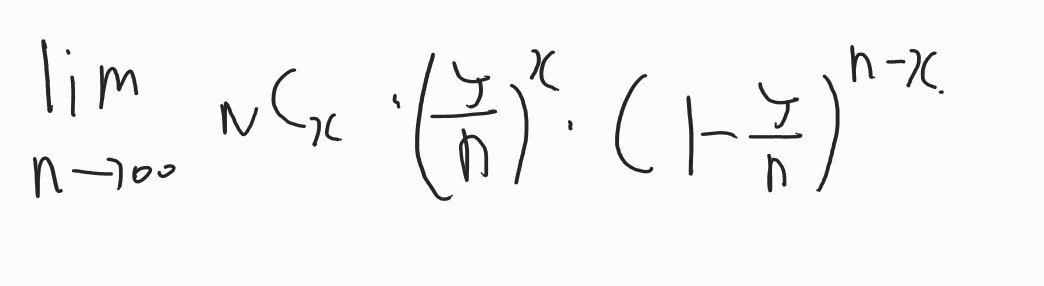
여기에서 확률 P는 각 구간에서 사건이 발생할 확률인 λ/N 가 되겠죠.
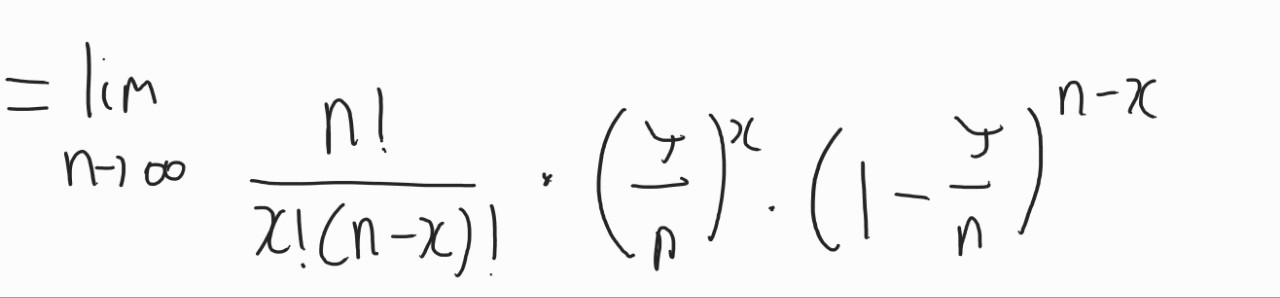

조합의 식을 정리해보면 위와 같이 나옵니다.
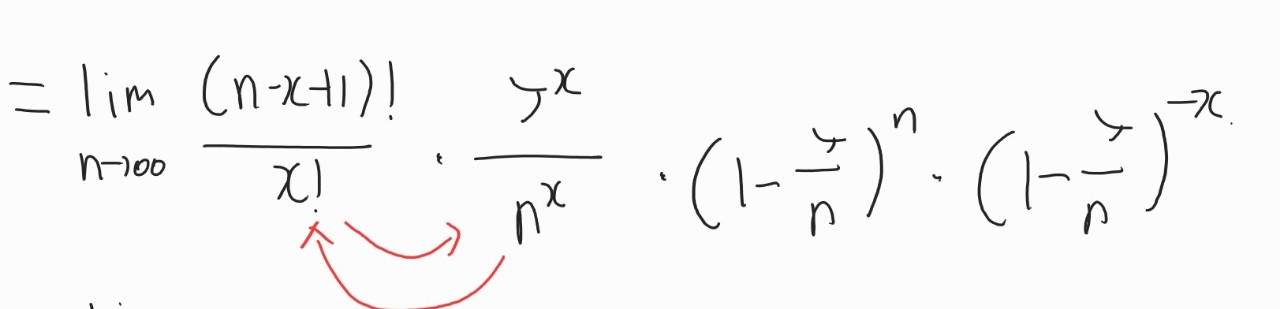
여기서 빨간색으로 표시한 X!과 n의 x승의 위치를 바꿔줍니다.
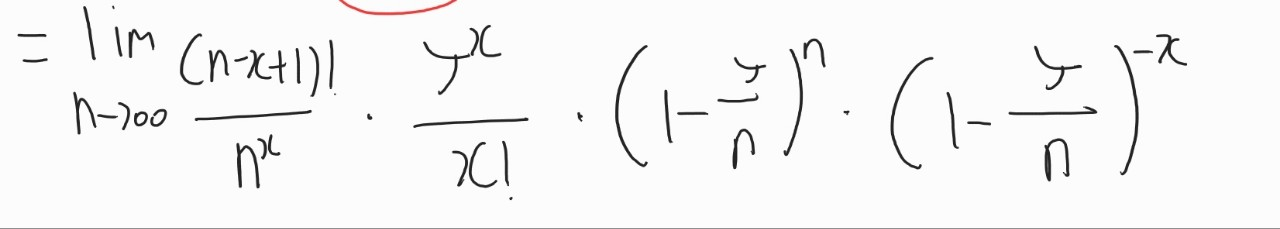
바꿔준 후, 첫번째 항에 대해서 N을 무한대로 보내보도록 하겠습니다.
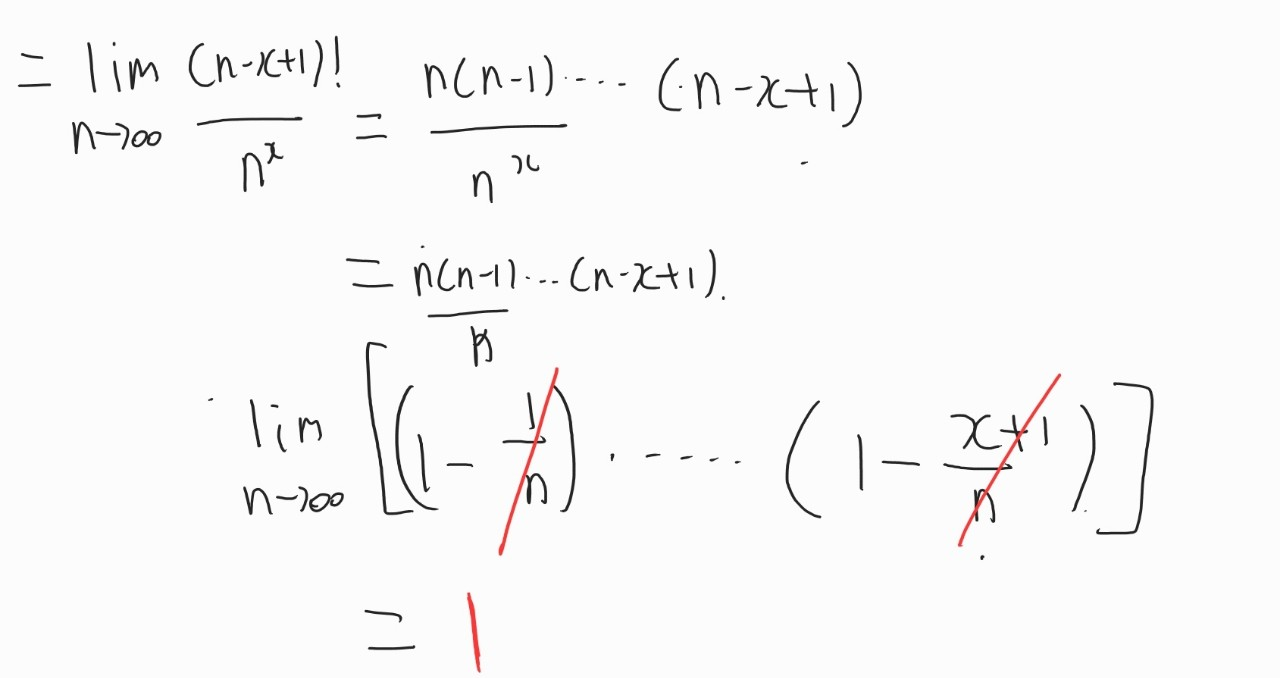
위 항에서 N을 무한대로 보내게 되면 1이 됩니다. 분자에서 n이 무조건 존재하기 때문에 약분으로 인하여 모든 항에 1이 남게 되고, 각 항을 곱하고, N을 무한대로 보내게 되면 결론적으로 1로 정리가됩니다.
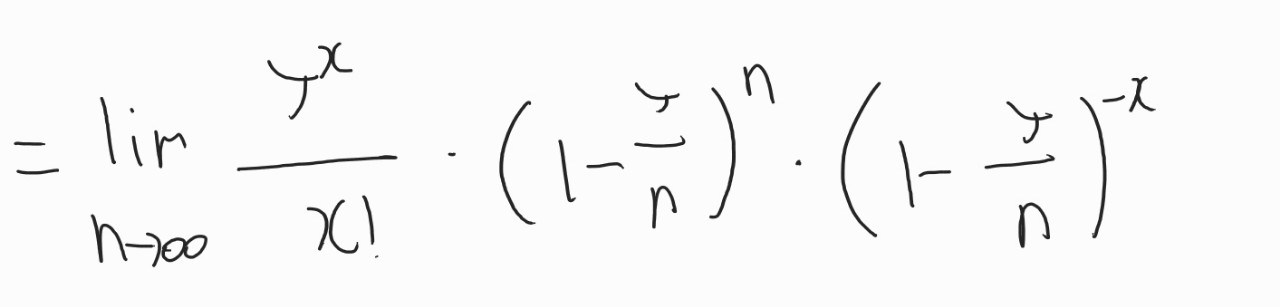
남은 항은 이렇게 되는데, 첫번째 항은 N이 없으므로, 두번째 항과 세번째 항에 대해서 N을 무한대로 보내보도록 하겠습니다.
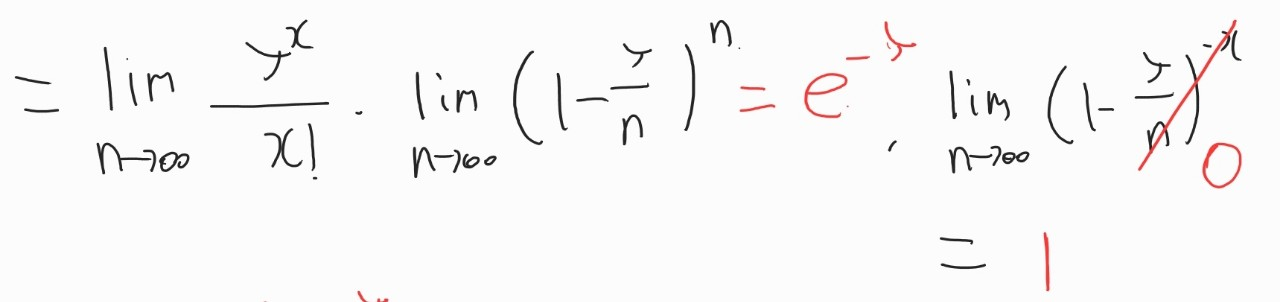
두번째 항은 지수함수의 극한 성질로 인하여 e의 -λ 제곱으로 정리가 되고, 세번째 항의 경우에는 1로 정리가 됩니다.
결론적으로 모든 식을 정리하게 되면 아래와 같이 됩니다.
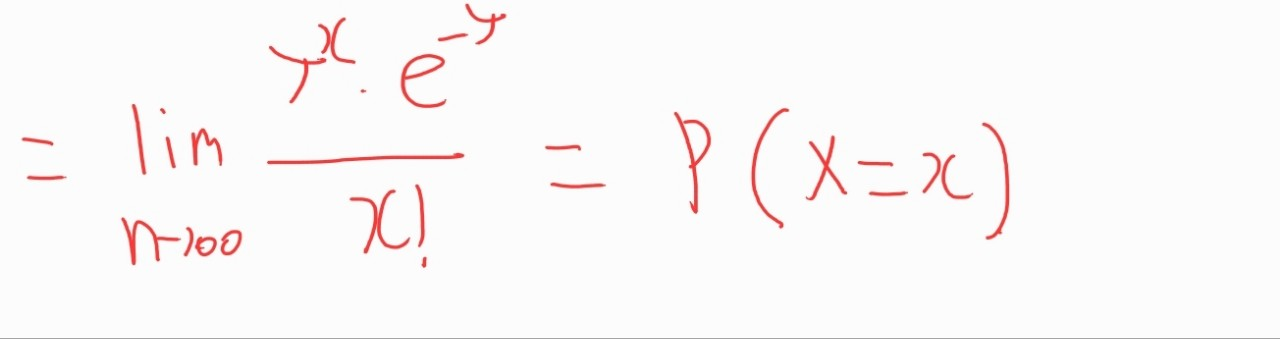
위 식이 바로 푸아송 분포에서의 확률 질량 함수입니다. 즉 사건 X가 발생할 확률이 되는거죠!
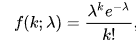
오늘은 푸아송 분포에 대해서 알아봤고, 확률 질량 함수를 유도해봤습니다. 다음 게시글에서는 푸아송 분포에서의 평균과 분산을 유도해보도록 하겠습니다.
'공부 > 통계학' 카테고리의 다른 글
| 지수 분포 (Exponential distribution) (0) | 2022.05.08 |
|---|---|
| [기초 통계학] 중심극한정리(Central limit theorem) (0) | 2021.11.13 |
| [기초 통계학] 불편성(Unbiased) (0) | 2021.11.10 |
| [기초 통계학] 표본평균과 표본 분산 (0) | 2021.11.09 |
| [기초통계학] 확률변수의 독립성 (0) | 2021.11.07 |

댓글